One small project I did was to code up a simulation of a growing tissue which feels pressure and where each cell has a dynamic state which depends on its neighbors and the pressure it feels. The idea is to reproduce some essential properties of morphogenesis. You can look at the code here. I am going to talk about the most interesting parts of the code.
I initialize the cells in an ordered lattice, with random perturbations in their positions, except those which are in the borders (bottom, left, right). Those are static and do not evolve in the simulation like the others. They are there just to represent the pressure from the rest of the body (huge) on the simulated tissue (tiny). This is not a very realistic assumption because many developmental systems have a size of the order of the body size, but we have to start somewhere!
All cells are connected with springs, which simulate adhesive and pressure forces in the tissue. If left alone, the system relaxes into a hexagonal configuration, since this minimises the spring potential energy. I integrate the harmonic oscillator equations using a fourth order Adams Moulton algorithm.
Now, it is important to realize that there are two time scales in the system: the pressure equilibration and cell lifetimes. We can assume the mechanical pressure equilibrates very fast, while cell divisions take their time. So what we do is run the oscillator system until equlibrium for each time step of the cellular state evolution, which we will talk about later.
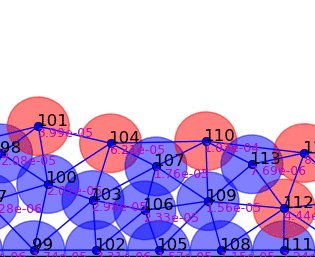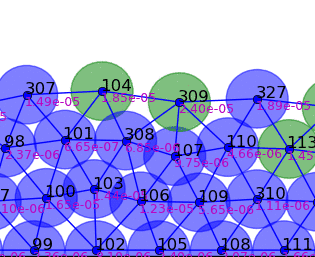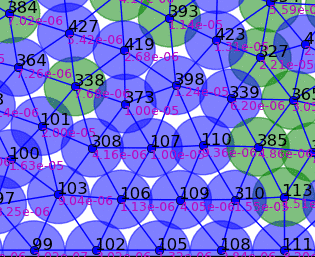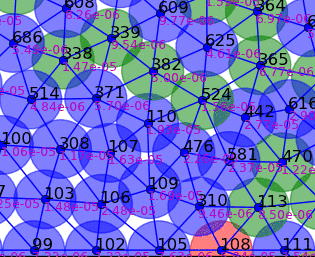
Springs connect each cell. The larger colored circle is of the same size as the rest length of the springs. Thus, overlapping circles mean the spring wants to extend, while spaces mean the spring wants to contract. The colors are explained below.
The mechanism for determining cell shape still has not been discussed. In this model, cell shape depends only on the relative positions of each of the points which represent a cell. This, combined with the spring model, allows us to efficiently calculate cell shape: we consider each point in space to belong to the cell represented by the spring endpoint which is closest to it in the sense of the euclidean metric. In other words, the tissue is represented by the
Voronoi tessellation of the point set which represents all cells. This might seem like an arbitrary choice, but further we will see that it in fact allows for a very powerful solution to an important problem: how do we connect the springs?
Since we do not directly simulate the cell shapes, but only the central points, there is no obvious solution to this problem without defining how cell shapes look like. Using the Voronoi tesselation is a good idea here because nearest neighbour connections are immediately available from the dual representation of the Voronoi tessellation, the Delaunay triangulation. This is a graph which connects only points which share a border in the Voronoi tessellation. Thus at each time step we can compute the Delaunay triangulation and obtain the links which should be represented by springs for the next time step.
At each time step, cells grow and the spring system is put into equilibrium. Then, the Delaunay triangulation is computed.
So what is the mechanical pressure in each cell? We now must turn to continuum mechanics for help. Cauchy’s stress tensor is defined at equilibrium by:
\[\int_V F_i + \int_S \sigma_{ij} = 0\]The usual approach is to use the divergence theorem to derive the relation
\[F_i + \sigma_{ij,j} = 0\]However the derivative of the stress tensor is of no use to us. What we want is a relation for the components of the stress tensor itself. We can use the fact that $F=-\nabla V$ to apply the divergence theorem the other way around:
\[V_i + \sigma_{ij} = 0\]V in our case is just the harmonic potential $kx^2$, so we know the tensor! But we actually want the total pressure for a cell, so we need some norm for the stress tensor. Appropriate measures would be its trace or its determinant. I chose to focus on the trace for simplicity. Because the stress tensor is fully determined from the elastic potential in our model, its trace over all components reduces to a sum over all components of the various potential terms. Thus it is sufficient to sum up the magnitudes of all potential terms to obtain the pressure, defined by
where the set ${j}$ denotes the neighbors for the $i$th cell. A problem with this model is that compressive vs. expansive pressure is not distinguished; this likely makes a big difference in real cells since they might divide if they feel expansion but not do so if they are compressed. So there is room for improvement here.
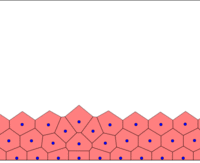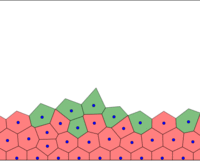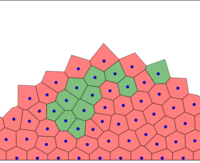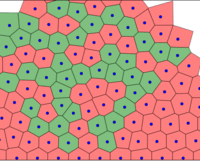
The full tissue evolving. Pressure is color coded.
Now we come to the part of simulating cell state. For now, we assume cells have discrete states and don’t have any preferential direction. This makes the model resemble Conway’s game of life, meaning that the next state of a given cell depends only on its current state and the sum of states of its the nearest neighbors (totalistic cellular automaton). For now the transitions are deterministic but they could be made probabilistic to make the model a bit more robust.
The transition table for the cellular automaton depends on three factors: the cell’s own state $x_i$, the pressure at the cell $p_i$ and the state of a cell’s neighbors $s_i=\sum_{{j}} x_j$ where the set ${j}$ denotes the neighbors for the $i$th cell. The pressure should be a binary variable and thus it will be defined by:
where $\nu$ is the calculated pressure value and $p_t$ is a predefined threshold. Since there are no more than 7 nearest neighbors for a cell, the variable $s_i\in S={0,1,…7}$, a set which has a cardinality of 8 and thus the total number of unique inputs are $(822=)$ 32. Thus there are $2^{32}$ possible transition tables. An additional table, which we will call the growth table, determines whether a cell will divide or not. It will have the same 32 inputs, thus there are again $2^{32}$ different rulesets.
The 4 possible inputs are color coded: blue, yellow, red and green. 2 states and two pressure values: high or low.
So there is a huge number of possible rules to go through. I let them all run on a cluster, but I can’t possibly visualize 65000 runs of the simulation so I took the opportunity to play around with Square’s crossfilter to visualize a data set with summary statistics for the whole simulation. You can look at that here. The non obvious quantities are the state entropy and the network entropy. They are just the Shannon entropy for the probability distributions of the cell’s binary state and the number of each cell’s spring connections. The first distribution relates to the automaton dynamics of the system: a system which is very non-uniform in state will have high entropy. The second relates to the lattice structure: a well ordered system will have most cells with 6 connections (hexagonal equilibrium packing) while a fast growing chaotic system will have various values for the connections and thus higher entropy.
Interestingly, I wrote the code for this simulation 3 times in an attempt to gain performance: first purely in python; then I rewrote the ODE equilibration routine in cython in an attempt to gain performance; and finally I just wrote the whole thing in c++ to be able to run it natively on our cluster. I was surprised by how easy it was to get cython up and running, and with a bit of tuning following their optimization guide I was able to get the routine to run really fast. The other interesting thing that surprised me was how fast I wrote the whole simulation in c++. I usually take a really long time writing down c++ code but since I knew exactly what to do it was really straightforward. So from now on always prototype in python, write later in c++.
In the end, this model proved a bit unsatisfactory, as not a lot of information could be gained from such a huge data set. In the future I plan to do a more deliberate search of function space, ‘intelligently designing’ cell outcomes.