Tiago Ramalho AI research in Tokyo
Fine-tune neural translation models with mBART
Jun 2020 by Tiago Ramalho
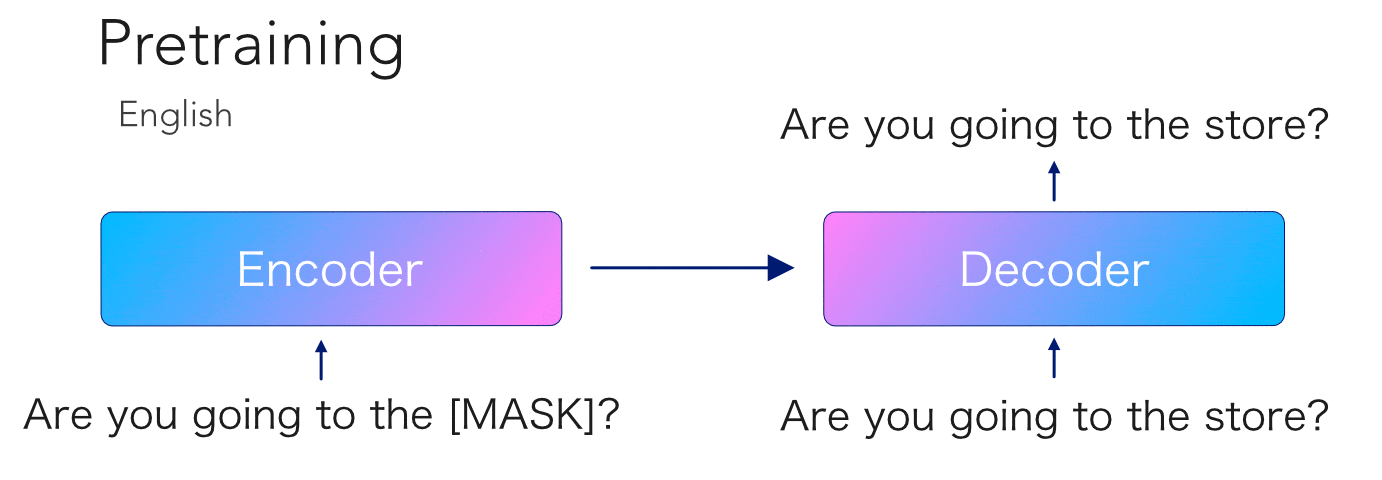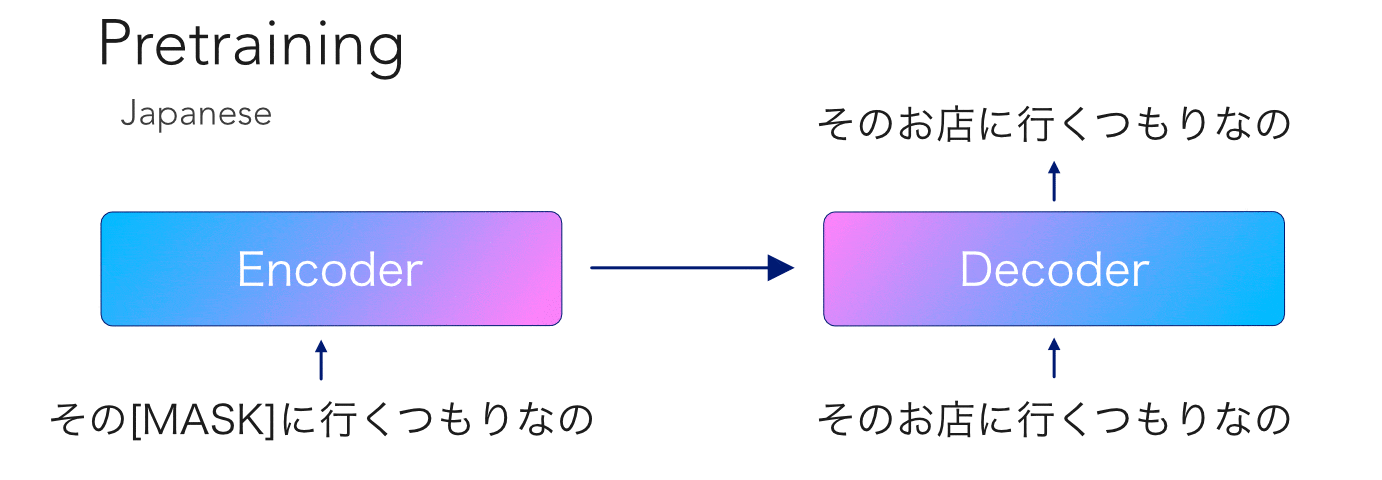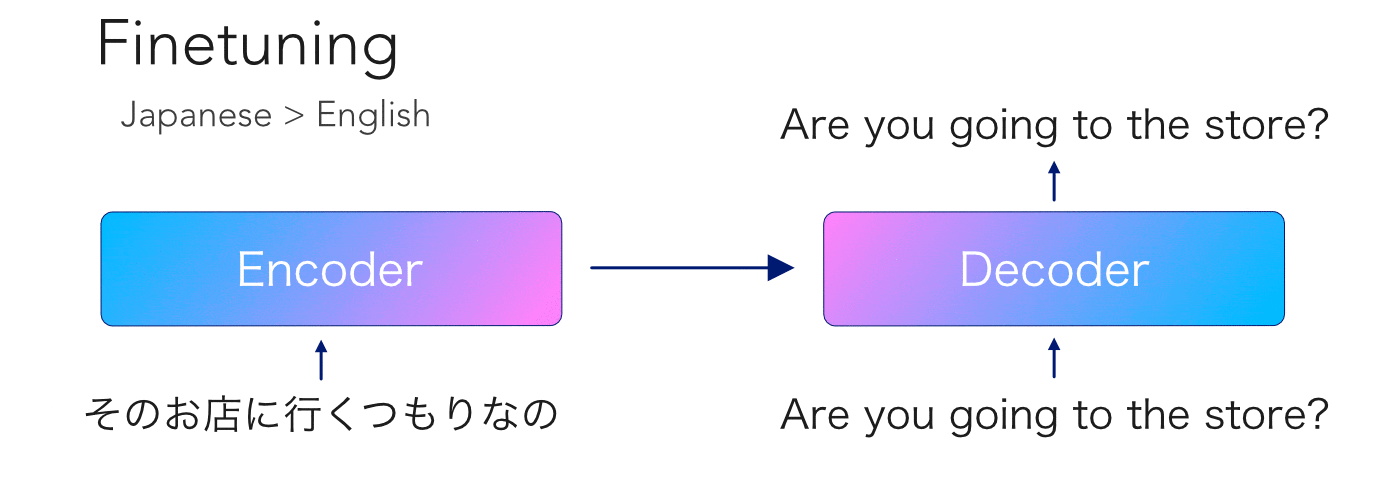mBART is another transformer model pretrained on so much data that no mortal would dare try to reproduce. This model is special because, like its unilingual cousin BART, it has an encoder-decoder architecture with an autoregressive decoder. Having been trained on 25 languages, this opens the door to a ton...
mBART is another transformer model pretrained on so much data that no mortal would dare try to reproduce. This model is special because, like its unilingual cousin BART, it has an encoder-decoder architecture with an autoregressive decoder. Having been trained on 25 languages, this opens the door to a ton...
Information Retrieval with Deep Neural Models
Jun 2020 by Tiago Ramalho
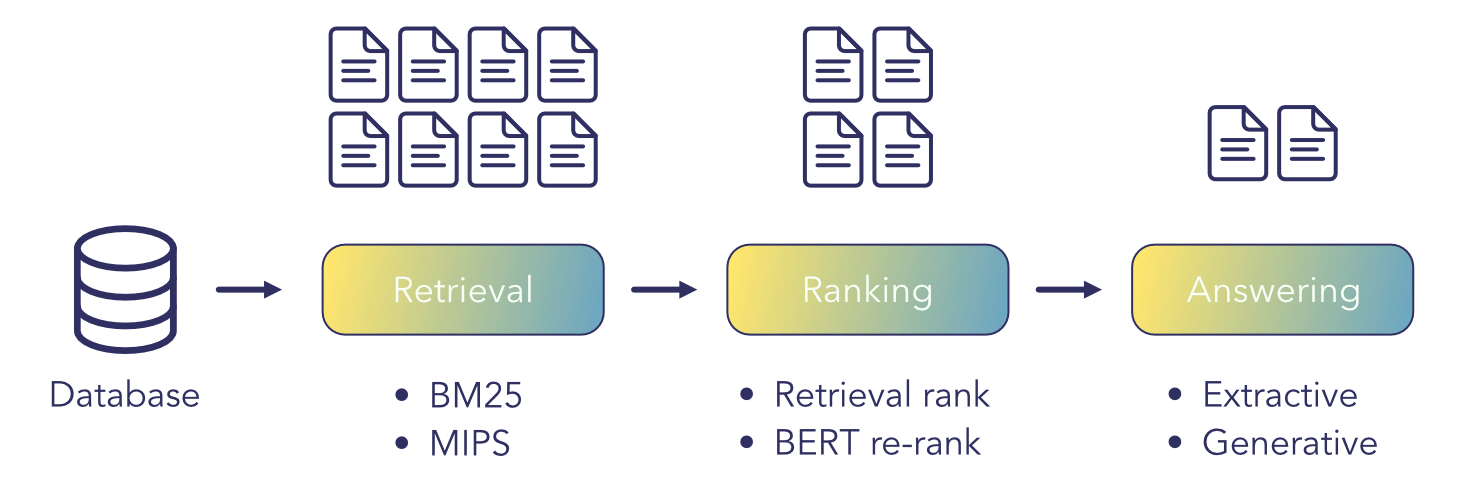Transformer based language models have achieved groundbreaking performance in almost all NLP tasks. So it is natural to think they can be used to improve textual search systems and information retrieval in general. Unlike what you may think, information retrieval is far from a solved problem. Suppose a query that’s...
Transformer based language models have achieved groundbreaking performance in almost all NLP tasks. So it is natural to think they can be used to improve textual search systems and information retrieval in general. Unlike what you may think, information retrieval is far from a solved problem. Suppose a query that’s...
Towards improved generalization in few-shot classification
Dec 2019 by Tiago Ramalho
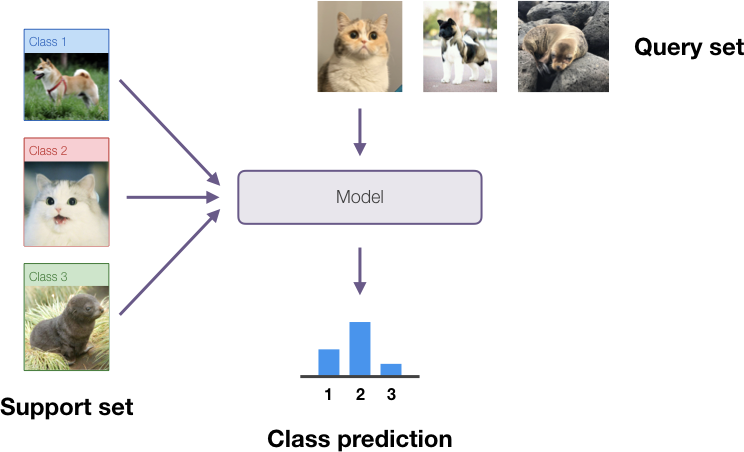While state of the art deep learning methods can come close to human performance on several tasks (i.e. classification), we know they are not very data efficient. A human can often generalize from a single instance of a class, while deep learning models need to see thousands of examples to...
While state of the art deep learning methods can come close to human performance on several tasks (i.e. classification), we know they are not very data efficient. A human can often generalize from a single instance of a class, while deep learning models need to see thousands of examples to...
Dimensionality reduction 101: linear algebra, hidden variables and generative models
Apr 2015 by Tiago Ramalho
Suppose you are faced with a high dimensional dataset and want to find some structure in the data: often there are only a few causes, but lots of different data points are generated due to noise corruption. How can we infer these causes? Here I’m going to cover the simplest method to...
Suppose you are faced with a high dimensional dataset and want to find some structure in the data: often there are only a few causes, but lots of different data points are generated due to noise corruption. How can we infer these causes? Here I’m going to cover the simplest method to...
Parallel programming with opencl and python: parallel scan
Jun 2014 by Tiago Ramalho
This post will continue the subject of how to implement common algorithms in a parallel processor, which I started to discuss here. Today we come to the second pattern, the scan. An example is the cumulative sum, where you iterate over an array and calculate the sum of all elements up...
This post will continue the subject of how to implement common algorithms in a parallel processor, which I started to discuss here. Today we come to the second pattern, the scan. An example is the cumulative sum, where you iterate over an array and calculate the sum of all elements up...
Older
Newer