This post will continue the subject of how to implement common algorithms in a parallel processor, which I started to discuss here. Today we come to the second pattern, the scan. An example is the cumulative sum, where you iterate over an array and calculate the sum of all elements up to the current one. Like reduce, the algorithm we’ll talk about is not exclusive for the sum operation, but for any binary associative operation (the max is another common example). There are two ways to do a parallel scan: the hills steele scan, which needs $\log n$ steps; and the blelloch scan, requiring $2 \log n$ steps. The blelloch scan is useful if you have more data than processors, because it only needs to do $\mathcal{O}(n)$ operations (this quantity is also referred to as the work efficiency); while the hillis steele scan needs $\mathcal{O}(n \log n)$ operations. So let’s look at how to implement both of them with opencl kernels.
Hillis Steele
This is the simplest scan to implement, and is also quite simple to understand. It is worthwhile noting that this is an inclusive scan, meaning the first element of the output array o is described as a function of the input array a as follows: \(o_i = \sum_{j=0}^i a_j\)
Naturally, you could replace the summation with any appropriate operator. Rather than describing the algorithm with words, I think a picture will make it much clearer than I could:
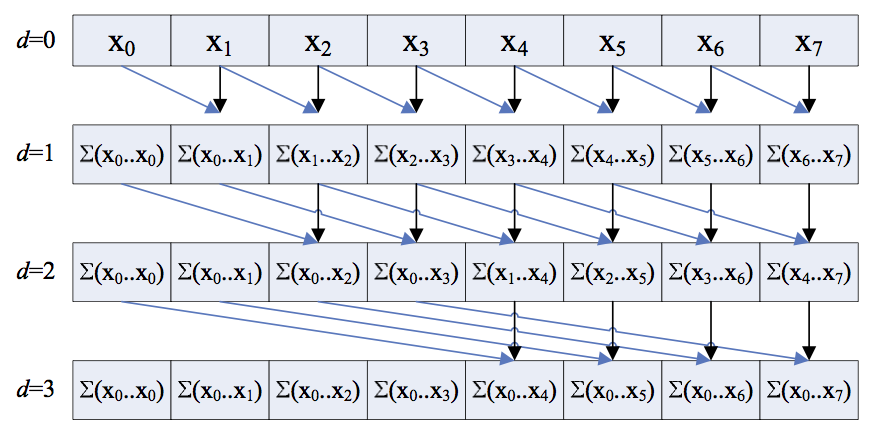
Visualization of the hillis steele inclusive scan. Credit: nvidia.
As you can see, the key is to add the value of your neighbor $2^d$ positions to your left to yourself, or just do nothing if such neighbor does not exist. This is quite simple to translate to an OpenCL kernel:
#define SWAP(a,b) {__local float *tmp=a;a=b;b=tmp;}
__kernel void scan(__global float *a,
__global float *r,
__local float *b,
__local float *c)
{
uint gid = get_global_id(0);
uint lid = get_local_id(0);
uint gs = get_local_size(0);
c[lid] = b[lid] = a[gid];
barrier(CLK_LOCAL_MEM_FENCE);
for(uint s = 1; s < gs; s <<= 1) {
if(lid > (s-1)) {
c[lid] = b[lid]+b[lid-s];
} else {
c[lid] = b[lid];
}
barrier(CLK_LOCAL_MEM_FENCE);
SWAP(b,c);
}
r[gid] = b[lid];
}
The for loop variable s represents the neighbor distance: it is multiplied by two every loop until we reach N neighbors. Note the use of the SWAP macro: it swaps the b and c pointers which will always denote the current step (c) and the previous step (b) without needing to copy memory.
Blelloch
The Blelloch scan is an exclusive scan, which means the sum is computed up to the current element but excluding it. In practice it means the result is the same as the inclusive scan, but shifted by one position to the right: \(o_i = \sum_{j=0}^{i-1} a_j,o_0=0\)
The idea of the algorithm is to avoid repeating summations of the same numbers. As an example, if you look at the picture above you can see that to calculate $o_5$ we need to add together ${x_5, x_4, x_2+x_3, x_1+x_0}$. That means we are essentially repeating the calculation of $o_3$ for nothing. So to avoid this we’d need to come up with a non overlapping set of partial sums that each calculation could reuse. That’s what this algorithm does!
As before, the algorithm is better explained with a picture or two:
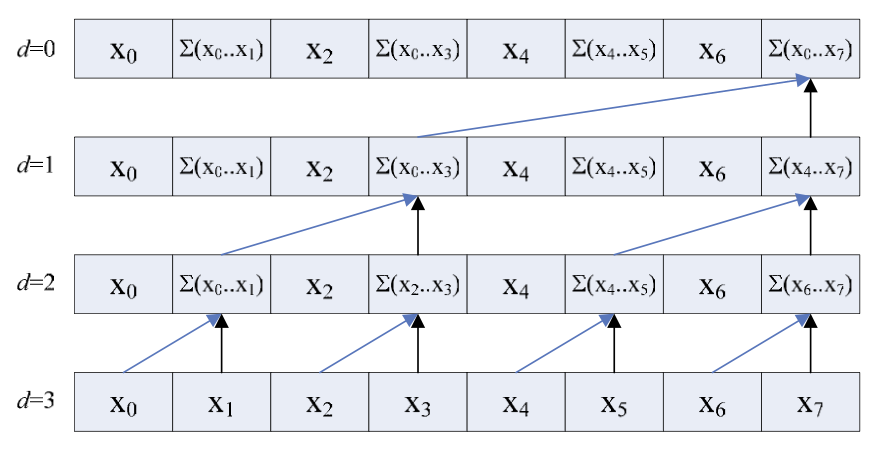
The up sweep portion of the Blelloch scan. Here the partial sums are calculated. Credit: nvidia.
The down sweep portion of the Blelloch scan. Here the partial sums are used to calculate the final answer.
You can see how the up sweep part consists of calculating partial sums, and the down sweep combines them in such a way that we end up with the correct results in the correct memory positions. Let’s see how to do this in OpenCL:
__kernel void scan(__global float *a,
__global float *r,
__local float *b,
uint n_items)
{
uint gid = get_global_id(0);
uint lid = get_local_id(0);
uint dp = 1;
b[2*lid] = a[2*gid];
b[2*lid+1] = a[2*gid+1];
for(uint s = n_items>>1; s > 0; s >>= 1) {
barrier(CLK_LOCAL_MEM_FENCE);
if(lid < s) {
uint i = dp*(2*lid+1)-1;
uint j = dp*(2*lid+2)-1;
b[j] += b[i];
}
dp <<= 1;
}
if(lid == 0) b[n_items - 1] = 0;
for(uint s = 1; s < n_items; s <<= 1) {
dp >>= 1;
barrier(CLK_LOCAL_MEM_FENCE);
if(lid < s) {
uint i = dp*(2*lid+1)-1;
uint j = dp*(2*lid+2)-1;
float t = b[j];
b[j] += b[i];
b[i] = t;
}
}
barrier(CLK_LOCAL_MEM_FENCE);
r[2*gid] = b[2*lid];
r[2*gid+1] = b[2*lid+1];
}
It took me a little while to wrap my head around both steps of the algorithm, but the end code is pretty similar to the Hillis Steele. There are two loops instead of one, and the indexing is a bit tricky, but I think that comparing the code to the picture it should be straightforward. You can also find a cuda version in the nvidia paper where I took the pictures from.