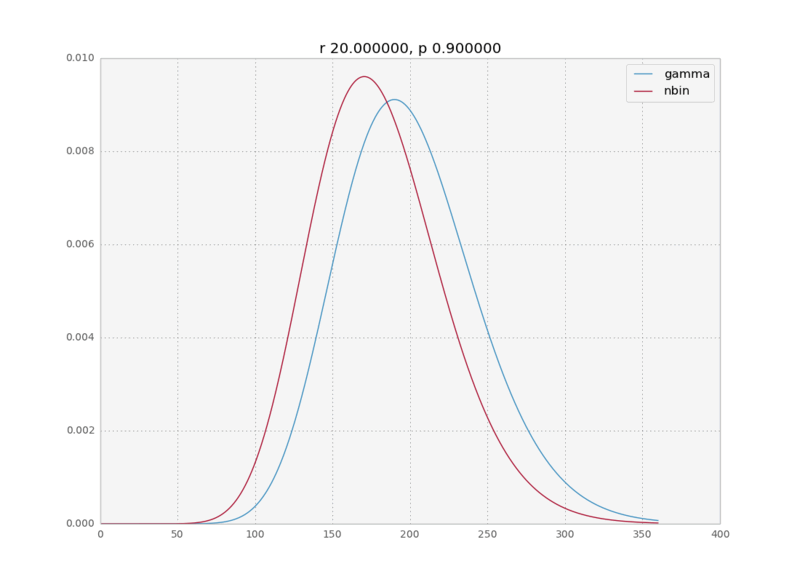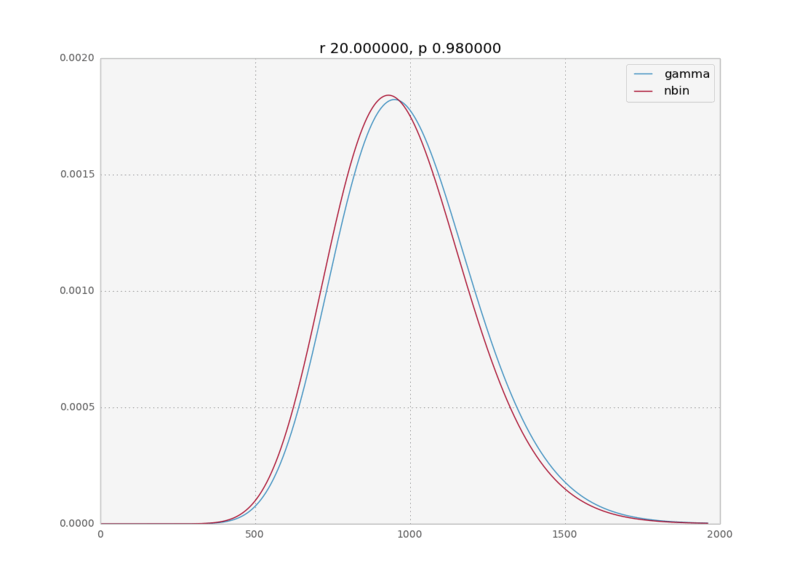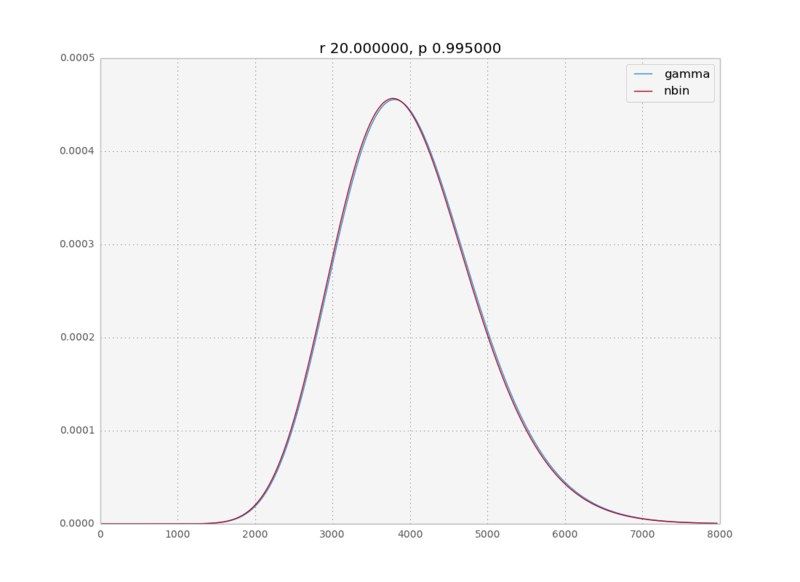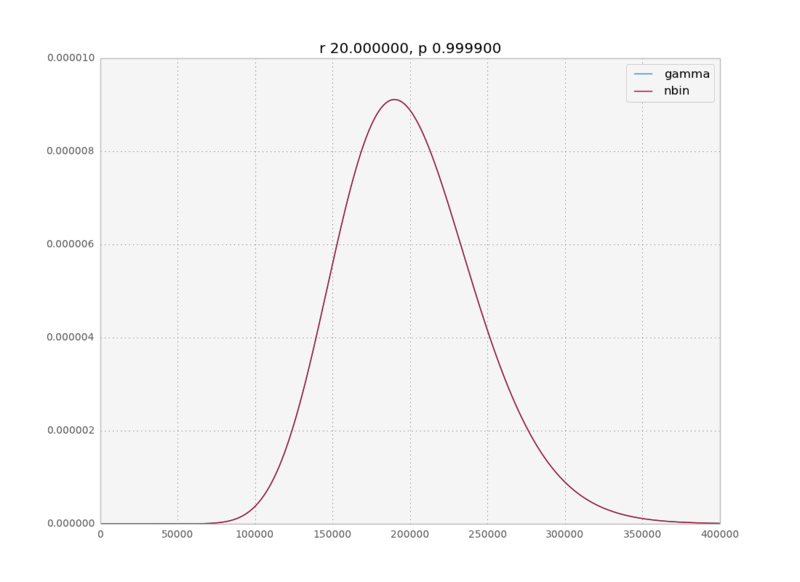
In a recent data analysis project I was fitting a negative binomial distribution to some data when I realized that the gamma distribution was an equally good fit. And with equally good I mean the MLE fits were numerically indistinguishable. This intrigued me. In the internet I could find only a cryptic sentence on wikipedia saying the negative binomial is a discrete analog to the gamma and a paper talking about bounds on how closely the negative binomial approximates the gamma, but nobody really explains why this is the case. So here is a quick physicist’s derivation of the limit for large k.
First let’s define the distributions: the negative binomial is defined as
with parameters $r,p$; and the gamma distribution is defined as
with parameters $\alpha, \beta$.
We assume $p\rightarrow 1$, therefore $\langle k \rangle = \frac{pr}{1-p} \rightarrow \infty$; which means that the values of $k$ for which $P(k)$ is non negligible will be very high.
Let’s start with the expression for the negative binomial and make the following replacement
(I actually derived this ansatz from the numerical fits). We get the following expression:
Let’s do stirling on both the denominator and numerator of the second term.
Let’s split the term $(k+\alpha-1)^{k+\alpha-1} = (k+\alpha-1)^k(k+\alpha-1)^{\alpha-1}$. We can simplify the first term as $(k+\alpha-1)^k = k^k\left(1+\frac{\alpha-1}{k}\right)^k$. The second term is approximately $k^{\alpha-1}$ because $k»\alpha-1$. Now the $e^k$ and $k^k$ cancel out and we get:
Now, remember that
We can use this on the two last terms of the expression to obtain $e^{\alpha-1}e^{-\beta k}$, which yields the gamma expression we were looking for.