Tiago Ramalho AI research in Tokyo
Parallel programming with opencl and python: parallel reduce
Jun 2014 by Tiago Ramalho
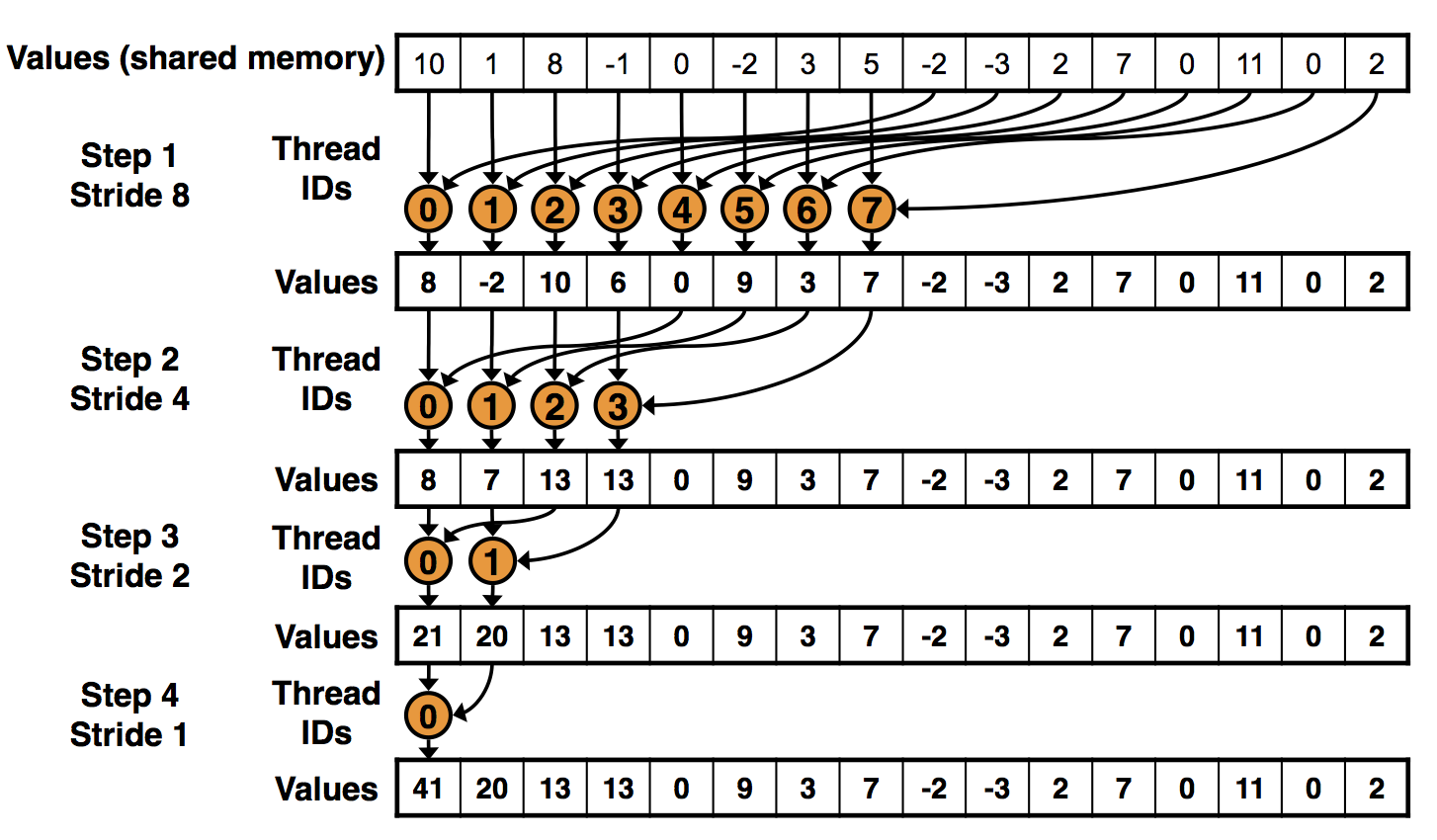Once you know how to use python to run opencl kernels on your device (read Part I and Part II of this series) you need to start thinking about the programming patterns you will use. While many tasks are inherently parallel (like calculating the value of a function for N...
Once you know how to use python to run opencl kernels on your device (read Part I and Part II of this series) you need to start thinking about the programming patterns you will use. While many tasks are inherently parallel (like calculating the value of a function for N...
Parallel programming with opencl and python: vectors and concurrency
May 2014 by Tiago Ramalho
Last time we saw how to run some simple code on the gpu. Now let’s look at some particular aspects related to parallel programming we should be aware of. Since gpus are massively parallel processors, you’d expect you could write your kernel code for a single data piece, and by...
Parallel programming with opencl and python
Apr 2014 by Tiago Ramalho
In the next few posts I’ll cover my experiences with learning how to program efficient parallel programs on gpus using opencl. Because the machine I got was a mac pro with the top of the line gpus (7 teraflops) I needed to use opencl, which is a bit complex and confusing...
How to fix scipys interpolating spline default behavior
Apr 2014 by Tiago Ramalho
Scipy’s UnivariateSpline class is a super useful way to smooth time series, especially if you need an estimate of the derivative. It is an implementation of an interpolating spline, which I’ve previously covered in this blog post. Its big problem is that the default parameters suck. Depending on the absolute...
Quick introduction to gaussian mixture models with python
Apr 2014 by Tiago Ramalho
Usually we like to model probability distributions with gaussian distributions. Not only are they the maximum entropy distributions if we only know the mean and variance of a dataset, the central limit theorem guarantees that random variables which are the result of summing many different random variables will be gaussian...